자바스크립트가 숫자를 저장하는 방법 (IEEE 754)

WEB/💡 Javascript

자바스크립트가 숫자를 저장하는 방법 (IEEE 754)

무딘붓 2024. 4. 28. 19:27

1. 개요

자바스크립트에서 0.1 + 0.2는 0.3이 아닙니다.

사실 알고 보면 C언어와 자바, 파이썬에서도 같은 오류가 발생합니다.

왜 이런 오류가 발생하고, 어떻게 정확한 실수 연산을 할 수 있을지 알아보도록 하겠습니다.

2. 자바스크립트가 숫자를 저장하는 방법

우선 자바스크립트에서는 숫자를 어떻게 저장하는지 알아보겠습니다.

자바스크립트는 C언어의 int, float, double처럼 실수와 정수를 구분하지 않고, 모든 숫자를 number 타입으로 저장합니다.

ECMAScript 사양에 따르면, number 타입은 IEEE 754 표준을 이용해 숫자를 저장합니다.

IEEE 754는 부동소수점을 표현하는 가장 널리 쓰이는 표준으로, C와 C++, Java의 double 타입, Python의 float 타입도 같은 표준을 사용합니다.

그렇다면 IEEE 754 표준으로 어떻게 숫자를 저장하는지 알아보겠습니다.

우선, IEEE 754는 32비트 단정밀도(single-precision), 64비트 배정밀도(double-precision)에 대한 부동소수점 형식을 지정하고 있습니다. 이 중에서 자바스크립트는 64비트 배정밀도 방식을 사용하여 정수와 부동소수점을 표기합니다.

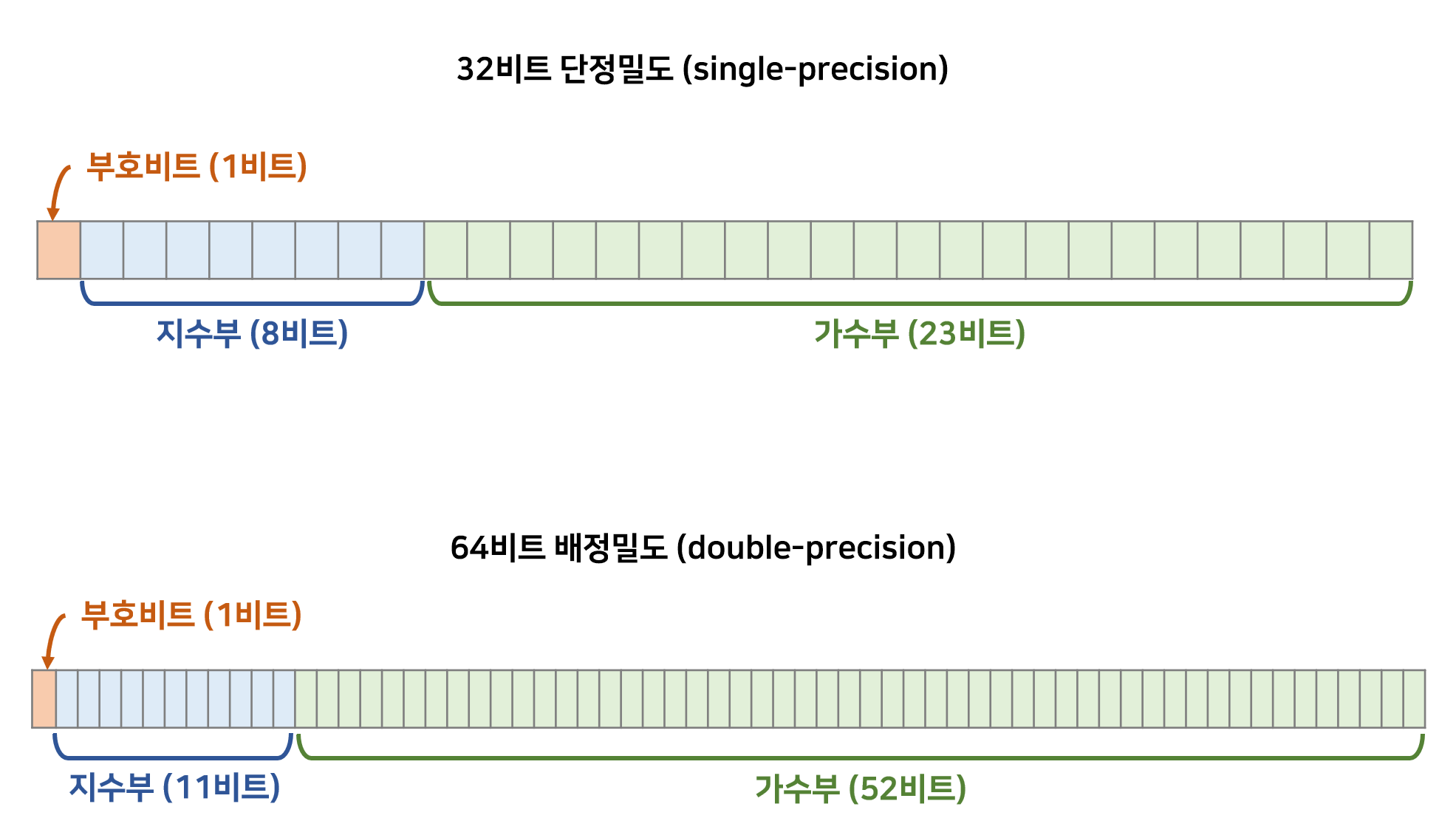
IEEE 754 부동소수점 표현은 크게 세 부분으로 구성되는데 부호 비트, 지수부, 가수부가 있습니다.

부호 부분(Sign)은 부호를 나타냅니다.
- 양수(0)인지 음수(1)인지를 나타내고 1비트를 사용합니다.
지수 부분(Exponent)은
- 32비트 단정밀도 방식에서 8비트
- 64비트 배정밀도 방식에서 11비트를 차지합니다.
가수 부분(Mantissa)은
- 32비트 단정밀도 방식에서 23비트
- 64비트 배정밀도 방식에서 52비트를 차지합니다.

각 부분에 어떤 값이 저장되는지 알기 위해, 실수를 IEEE 754 부동소수점 방식으로 표현하는 과정을 살펴보겠습니다.

10000.625 라는 숫자를 예로 들어 표현해 보면

10000.625를 이진수로 변환합니다.
- → 10 0111 0001 0000.101
부동 소수점 형식으로 정규화
- → 1.0011100010000101 x 2^13
지수부 11비트는
- 13+1023=1036
  - (지수가 -인 경우가 있으니까 +1023을 해준다)
  - (즉, 지수가 2^0이면 0+1023=1023)
- → 2진수로 변환하면 1000 0001 100
나머지 가수부는
- 소수점 이하자리 “0011 1000 1000 0101”
- 가수부 52비트의 나머지 자리는 0으로 채운다.
- → 0011 1000 1000 0101 0000 0000 0000 0000 0000 0000 0000 0000 0000
부호비트는
- 양수니까 0

따라서, 10000.625를 부정밀도 64비트 부동소수점 형식으로 나타내면

0 1000 0001 100 0011 1000 1000 0101 0000 0000 0000 0000 0000 0000 0000 0000 0000

과 같이 변환됩니다.

3. 0.1+0.2 계산해 보기

이제 IEEE 754 64비트 부동소수점으로 숫자를 저장하는 법을 배웠으니, 0.1+0.2 계산을 해보겠습니다.

우선 0.1을 저장해 봅시다.

이진수로 변환
- → 0.000110011… (순환소수!)
부동 소수점 형식으로 정규화
- → 1.10011… x 2^-4
지수부 11비트는
- -4 + 1023 = 1019
- → 2진수로 변환하면 1111 1110 11
- → 지수부는 11비트이므로 앞에 0을 붙여서 0111 1111 011
나머지 가수부는
- 소수점 이하 52자리는
- 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 …
- 53번째 자리에는 1이 들어가므로, 이를 반올림하면 아래와 같습니다.
- 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1010
  - ( 반올림 규칙은 https://en.wikipedia.org/wiki/IEEE_754#Rounding_rules 를 참고하세요)
- → 따라서, 가수부는 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1010
부호비트는
- 양수니까 0

따라서 0.1은 0 0111 1111 011 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1010 과 같은 형태로 저장되게 됩니다.

이진수로 변환하는 과정에서 순환소수가 되기 때문에, 가수부가 정확한 값을 저장하지 못한다는 점을 기억해 주세요.

마찬가지로 0.2도 저장해 봅시다.

이진수로 변환
- → 0.00110011001… (순환소수!)
부동 소수점 형식으로 정규화
- → 1.10011001… x 2^-3
지수부 11비트는
- -3 + 1023 = 1020
- → 2진수로 변환하면 1111 1111 00
- → 지수부는 11비트이므로 앞에 0을 붙여서 0111 1111 100
나머지 가수부는
- 소수점 이하 52자리는
- 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 …
- → 0.1과 동일하므로, 가수부는 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1010
부호비트는
- 양수니까 0

0.2는 0 0111 1111 100 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1010 으로 저장됩니다.

이제 두 수를 더해보겠습니다.

64비트로 저장된 0.1을 다시 이진수로 복원해 봅시다.

0.1 → 0 0111 1111 011 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1010
1.1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1010 x 2^-4
= 0. 0001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1010
= 0. 0001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 101

같은 방법으로 0.2도 다시 이진수로 복원해 보겠습니다.

0.2 → 0 0111 1111 100 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1010
1.1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1010 x 2^-3
= 0. 001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1010
= 0. 001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 101

이제 두 수를 더해봅시다.

  0.0001100110011001100110011001100110011001100110011001101
+ 0.001100110011001100110011001100110011001100110011001101
= 0.0100110011001100110011001100110011001100110011001100111

더한 값은 이진수로 0.0100110011001100110011001100110011001100110011001100111 입니다.

이를 10진수로 다시 변환하면 0.30000000000000004 즉, 자바스크립트에서 0.1+0.2를 계산한 결과 값이 나옵니다.

4. 결론 요약과 해결 방법

0.1과 0.2를 더했을 때 0.3이 나오지 않는 이유를 간략히 요약해 보겠습니다.

JavaScript는 숫자를 IEEE 754에 정의된 64비트 부동소수점 형식으로 저장한다.
부동소수점 형식으로 변환하는 과정에서 0.1과 같은 숫자는 2진수로 변환할 때 순환소수가 된다.
따라서, 0.1과 같은 값은 정확히 64비트 안에 저장하지 못하고, 반올림 후 저장해서 오차가 발생한다.
이러한 오차가 0.1+0.2 같은 연산의 오차를 만든다.

그렇다면 0.1 + 0.2와 같은 계산을 오차 없이 하려면 어떻게 해야 할까요?

자바스크립트에서는 다음과 같은 방법들로 해결할 수 있습니다.

1 ) 정수로 변환해서 계산하기

문제가 생기는 값을 모두 정수로 변환해서 계산하는 방법입니다. 정수로 변환한 후에는 오차가 사라지므로, 연산 후에도 오차가 발생하지 않습니다.

다만 두 수를 정수로 만드는 과정과 다시 돌려놓는 과정이 번거로울 수 있습니다.

let result = (0.1 * 10 + 0.2 * 10) / 10; // result는 0.3이 된다.

2 ) 소수점 자릿수 제한

원하는 소수점 이하 자릿수로 숫자를 반올림하여 계산하는 방법입니다.

let result = (0.1 + 0.2).toFixed(1); // result는 문자열 "0.3"이  된다.

3 ) Number.EPSILON

ES6에서 도입된 Number. EPSILON은 1과 1보다 큰 가장 작은 부동 소수점 수 사이의 차이를 나타내는 값입니다.

실제 값은 2.2204460492503130808472633361816 × 10-16으로, 부동소수점으로 인해 발생하는 오차를 해결하기 위해 사용합니다.

Number. EPSILON을 사용하여 부동소수점을 비교하는 예시는 다음과 같습니다.

function isEqual(a, b){
	// a와 b를 뺀 값의 절대값이 Number.EPSILON보다 작으면 같은 수로 판단.
	return Math.abs(a - b) < Number.EPSILON;
}
isEqual(0.1 + 0.2, 0.3); // true

4) 외부 라이브러리 사용

decimal.js 나 big.js와 같은 외부 라이브러리를 사용하는 방법도 있습니다.

이런 라이브러리는 부동소수점으로 인한 문제를 해결하기 위해 0.1과 같은 값을 부동소수점 형식으로 저장하지 않고, 1/10 과 같이 고정된 정수값으로 표현합니다.

사용하는 방법은 다음과 같습니다.

// Decimal.js 사용 예시
const Decimal = require('decimal.js');

const result = new Decimal('0.1').plus('0.2'); // result는 0.3이 된다.

// Big.js 사용 예시
const Big = require('big.js');

const a = new Big(0.1);
const b = new Big(0.2);
const result = a.plus(b); // result는 0.3이 된다.

참고자료

저작자표시

'WEB > 💡 Javascript' 카테고리의 다른 글

[JavaScript] 비교적 정확한 타이머 만들기 (0)	2024.08.15
[Javascript] HTML 페이지에 TOC(Table of Content, 목차) 만들기 (0)	2024.07.12
[Javascript] 마이크 변경과 볼륨 조절하기 (0)	2024.03.23
[Javascript] 역따옴표(백틱)을 이용한 템플릿 리터럴(template literal) (0)	2022.07.27
[Javascript] '=='와 '==='의 차이점 (0)	2022.07.27

현재글자바스크립트가 숫자를 저장하는 방법 (IEEE 754)

무딘붓의 코딩기록